A paper titled “Eigenvectors from eigenvalues” has recently sparkled heated discussions in Chinese communities on Wechat. This paper, co-authored by Peter Denton, Stephen Parke, Terence Tao and Xining Zhang, introduces a new method for calculating eigenvectors from solely eigenvalues. Some bloggers even describe this method as a revolution to traditional textbook method for calculating eigenvectors. I’ve never heard of this method before and wanted to give it a try to see if it is valid from a computational aspect.
This method has a simple mathematical form as below. It can be found on Terence Tao’s blog post.
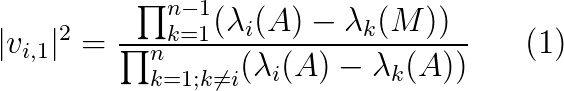
It basically says the eigenvalues of a Hermitian matrix can be calculated directly from its eigenvalues and eigenvalues of some of its submatrices using this formula. The submatrices are obtained by deleting the j-th row and column from the original matrix, where j ranges from 1 up to the N, the dimension of the matrix. From a computational view, it’s unlikely that this formula would accelerate the calculation of eigenvectors because of the extra cost of calculating the eigenvalues of N submatrices of similar size. Let’s find out if this is the case.
There are convinient functions (linalg.eig, linalg.eigsh, linalg.eigvals, etc) in numpy to calculate eigenvalues and eigenvectors. All these functions calculate both values at the same time. The differences may be that some of them don’t return eigenvectors. The implementation is actually not hard, I try to use vectorization as much as possible. To make the execution time comparable, I also assume the eigenvalues of the original matrix are given for this new method.
1A = np.random.rand(16).reshape((4, 4))
2A = A + A.T # a symmetric real matrix is a hermitian matrix
3n = A.shape[0]
4
5eval_A, evec_A = np.linalg.eig(A)
6
7# Numpy way of calculating eigen vector
8def evec_from_numpy(A):
9 _, evec_A = np.linalg.eig(A)
10 return evec_A
11
12# Let's assume we have already know eval_A but not evec_A
13def evec_from_eval(A, eval_A):
14 n = A.shape[0]
15 evec_A = np.zeros((n, n))
16 for k in range(n):
17 M = np.delete(A, k, axis=0)
18 M = np.delete(M, k, axis=1)
19 eval_M = np.linalg.eigvals(M)
20
21 nominator = [np.prod(eval_A[i] - eval_M) for i in range(n)]
22 denominator = [np.prod(np.delete(eval_A[i] - eval_A, i)) for i in range(n)]
23
24 evec_A[k, :] = np.array(nominator) / np.array(denominator)
25 return evec_A
26
27evec_A_from_eval = np.zeros((n, n))
28evec_A_from_eval = evec_from_eval(A, eval_A)
29
30print(evec_A_from_eval)
31print(evec_A**2)
32
33np.allclose(evec_A_from_eval, evec_A**2)
34
35> [[0.22970996 0.35544925 0.34406204 0.07077875]
36 [0.32054667 0.02114573 0.33018477 0.32812283]
37 [0.16357732 0.15884734 0.1701387 0.50743663]
38 [0.28616604 0.46455768 0.15561449 0.09366179]]
39> [[0.22970996 0.35544925 0.34406204 0.07077875]
40 [0.32054667 0.02114573 0.33018477 0.32812283]
41 [0.16357732 0.15884734 0.1701387 0.50743663]
42 [0.28616604 0.46455768 0.15561449 0.09366179]]
43> TrueSo the implemenation gives the same results as the numpy functions. Next question is how fast it can be?
1# This test is performed on a 10 by 10 matrix A
2def evaluate_execution_time_1():
3 [evec_from_numpy(A) for i in range(100)]
4
5def evaluate_execution_time_2():
6 [evec_from_eval(A, eval_A) for i in range(100)]
7
8time evaluate_execution_time_1()
9> CPU times: user 7.48 ms, sys: 2.45 ms, total: 9.93 ms
10Wall time: 11.2 ms
11
12time evaluate_execution_time_2()
13> CPU times: user 248 ms, sys: 2.99 ms, total: 251 ms
14Wall time: 249 msAs our expectation, the new method of my implemetation is much slower than the numpy one. Unless there exists a fast way to directly calculate eigenvalues, this new method can hardly beat the traditional one, in my opinion.
It turns out the method proposed by this paper is not new. Since it was published this August, many people have claimed that they have discovered it much earlier in their paper/books, though in different forms of the equation. Even Terance himself admitted that he will re-write this paper to make it a historical review of all related findings. More infomation can be found in the discussion under his post. My take here is that mathematics has become such an intricate field with unimaginable breadth and depth, doing math research is likely to constantly re-discover what other people have already found.