Months ago I had this question of comparing TADs from two Hi-C experiments in my research. TAD is short for topologically associated domains, discovered by Dixon et al [1] in 2012, which are regions in the genome that interacts more frequenctly with regions in the domain than outside. The goal of comparing TADs from two Hi-C expriments is to search for differentially interacting regions under two conditions to tease out regions that react to the conditions.
When I first thought about this question, I felt that comparing TADs is not well-defined. Let’s put aside the specific differentially-interacting regions. Sometimes we might be interesting to know the overall similarity of two sets of TADs from two conditions. For example, TADs called from two biological replicates should have a high similarity. I have no clue on how to measure the similarity of two sets of TADs until I came across this paper[2] the other day. In this paper, Yu et al. introduced two metrics, Variation of Information (VI) and Jaccard Index, to do this.
A set of TADs are composed of continous or discrete genomic regions like below:
chr1 40000 160000
chr1 22000000 24320000
…
chrX 5800000 7600000
The Variation of Information proposed by Marina Meila[3] measures the similarity of two disjoint partitions of a given set. A disjoint partition of a set has the property that any two subsets have no common elements. Let’s assume {C1, C2, …, Ck} is a disjoint partition of set C. If we randomly pick an element from C, the probability that it belongs to Ck is:
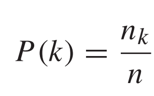
The overall uncertainty of the partition is equal to the entropy of the probability distribution.
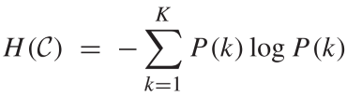
Now if we have a second partition C’ of C, {C’1, C’2, …, C’k}. We can define the mutual information between them as below.
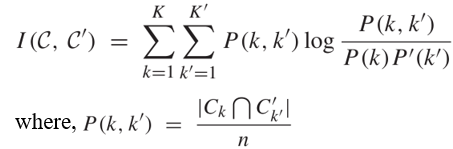
Here is a nice explanation of above equation from Marina Meila:
Intuitively, we can think of I(C, C’) in the following way: we are given a random point in D. The uncertainty about its cluster in C’ is measured by H(C’). Suppose now that we are told which cluster the point belongs to in C. How much does this knowledge reduce the uncertainty abuot C’? This reduction in uncertainty, averaged over all points, is equal to I(C, C’).
Then the VI is defined as follows.
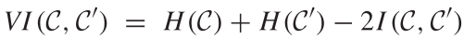
Below is a simplified and faster way to calculate VI suggested by Yu et al[2].
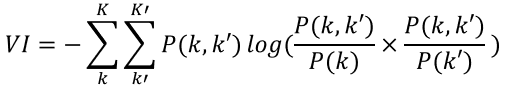
Note that VI is non-negative and has an upper bound of log(n) where n is the number of elements in C. Because VI only applies to disjoint partition of a set, while TAD can be hierarchical and nested (subTADs) in nature, VI is not suitable for subTADs. Jaccard Index has no such limitations and can be used for two sets of subTADs. Jaccard Index can be simply thought as the intersection over union. It is widely used to evaluate the similarity of two clusterings.
In practice, each TAD consists of multiple 40kb bins (or any resolution specified when TAD is called). I treated each bin as an element of a TAD set, then a TAD set of a given genome can be looked as a partition of genome-wide 40kb bins. Below I show an example of calculating VI and Jaccard Index.
1def readTAD(file):
2 tad_set = []
3 with open(file, 'r') as f:
4 for line in f:
5 tmp_set = set()
6 line = line.strip().split()
7 for i in range(int(line[1]), int(line[2]), 40000):
8 tmp_set.add(line[0]+'-'+str(i))
9 tad_set.append(tmp_set)
10 return tad_set
11
12# Important sanity check step to make sure two TAD sets consisting of the same set of 40kb bins.
13def commonBins(tad1, tad2):
14 s1 = reduce((lambda x, y: x.union(y)), tad1)
15 s2 = reduce((lambda x, y: x.union(y)), tad2)
16 s1_2 = s1.intersection(s2)
17 s1 = []
18 s2 = []
19 for s in tad1:
20 s_tmp = s.intersection(s1_2)
21 if len(s_tmp):
22 s1.append(s_tmp)
23 for s in tad2:
24 s_tmp = s.intersection(s1_2)
25 if len(s_tmp):
26 s2.append(s_tmp)
27 return s1, s2
28
29def VIforTADs(tad1, tad2):
30 ## simplified version of calculation: VI = -sigma P(k, k')*log{ P(k, k')**2/( P(k)P(k') ) }
31 ## P(k) = nk/n
32 ## P(k, k') = |intersect(Ck, C'k')| / n
33 n1 = reduce((lambda x, y: x+y), [len(x) for x in tad1])
34 n2 = reduce((lambda x, y: x+y), [len(x) for x in tad2])
35 n = max(n1, n2)
36 VI = 0
37 for s1 in tad1:
38 for s2 in tad2:
39 Pkk = float(len(s1.intersection(s2)))/n
40 if Pkk > 0:
41 VI += -Pkk * log10( (Pkk**2)/(float(len(s1) * len(s2))/(n**2)) )
42 print VI, log10(n) ## VI <= log(n)
43 return VI
44
45def JIforTADs(tad1, tad2):
46 maxJI = 0
47 n = len(tad1)
48 m = len(tad2)
49 ji = np.zeros((n, m))
50 for i in range(n):
51 for j in range(m):
52 ji[i, j] = len(tad1[i].intersection(tad2[j])) / float(len(tad1[i].union(tad2[j])))
53 row_max_sum = np.sum(np.amax(ji, axis=1)) # find the TAD in B that has the maximum JI with a TAD in A
54 col_max_sum = np.sum(np.amax(ji, axis=0)) # find the TAD in A that has the maximum JI with a TAD in B
55 return (row_max_sum + col_max_sum)/(m+n)
56
57tad1 = readTAD('exp_1.40kb.iced.domains')
58tad2 = readTAD('exp_2.40kb.iced.domains')
59tad1, tad2 = commonBins(tad1, tad2)
60
61VIforTADs(tad1, tad2)
62# 0.0649948733336 4.81281980622
63
64JIforTADs(tad1, tad2)
65# 0.8993629455535996Reference:
[1]. Dixon et al. (2012). Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature.
[2]. Yu et al. (2018). Identifying topologically associating domains and subdomains by Gaussian Mixture model And Proportion Test. Nature Communications.
[3]. Meila, Marina. (2007). Comparing clusterings - an information based distance. Journal of Multivariate Analysis.