String matching algorithms are used in lots of scenarios such as searching words in a text file, or locating specific sequences in a genome. I’ve heard of KMP algorithm long time ago, but don’t have a chance to implement it by myself (just lazy). It seems that KMP is not widely used in genomics field, but instead another algorithm, Boyer-Moore, is taught more often in computational genomics classes. I recently find a great online tutorial on computational genomics by Ben Langmead @JHU (link). In the string exact matching section, Ben talks about the idea behind Boyer-Moore and kindly provides a python implementation which was based on the Z algorithm and Dan Gusfield’s book. Like other teaching materials, Dan’s book first looked at the naive approach for exact matching. But then this book went straightly into the Z algorithm, with which it nicely linked Boyer-Moore and KMP algorithms. For the first time, I know that both algorithms can be derived from the Z algorithm.
What interests me more is that this book mentions that KMP, while widely-known, is much inferior to the Boyer-Moore algorithm in practice. I can’t help asking myself: Is that really the case? This question motivates me to run some tests on the two algorithms and write this article.
First, let’s briefly go over the two string-matching algorithms. Unlike the naive algorithm which takes O(N*M) time, Boyer-Moore and KMP require only linear time to find all matches of a pattern in a string. What makes Boyer-Moore and KMP fast is the pre-processing of the pattern, which can be used to skip characters during the comparison. The pre-processing used by KMP is to calculate an array of the length of longest prefix suffix at each position of the pattern.
LPS array: the longest suffix of substring P[0..i] which is also a prefix of P, where P denotes a pattern of length n and i the i-th position.
As described in Dan’s book, LPS array can be derived from Z algorithm, which I refer to as KMP-Z-based. However, the more commonly-known method to calculate this array is without Z algorithm (as in most textbooks), I’ll call this method as KMP-vanilla. In this article, I’ll use Z algorithm to illustrate KMP and Boyer-Moore methods, as in Dan’s book.
The Z algorithm itself is a string matching method which also requires linear time to find all matches. It first calculates a Z array, which is the longest prefix of substring P[i..(n-1)] which is also a prefix of P. To find the matches using Z algorithm, you can use a trick that stitches the pattern to the start of the target string and the Z array for the new string would tell you where the pattern is found in the target string.
Z array: the longest prefix of substring P[i..(n-1)] which is also a prefix of P.
You can see the link between Z array and the longest prefix suffix (LPS) array, and how one can obtain the LPS array from Z array. For more details on implementation, I’ve implemented a C++ version of both Z-based KMP and vanilla KMP at my GitHub.
Boyer-Moore algorithm is different from KMP such that it compares the pattern and target string from right to left. Other than that, it uses different preprocessing strategies, which are called the bad character rule and good suffix rule (For more details, please refer to Ben’s tutorial). The bad character rule finds the nearest character to the mismatched one in the pattern that matches the mismatched character in the target string. For example, if the character “x” is mismatched with the “a” in the pattern, then the pattern should shift to the nearest “x” before “a” for comparison. We can see the bad character rule also utilizes the information from the target string to accelerate matching.
1
2Bad character rule finds the nearest x matches the target string
3S: - - - - - b b (x)
4 |
5P: b b - (x) - b b aThe good suffix rule, on the other hand, looks for a substring (need not to a prefix) of P[0..(i-1)] that matches a suffix of the P[0..(i-1)], where i is the mismatched position. The good suffix rule is, in some sense, similar to the LPS array which is a preprocessing of the pattern only. A stronger version of it also requires the character after the substring does not match P[i] since P[i] is a mismatch to the target string. For an C++ implementation of Boyer-Moore, please refer to my GitHub.
1
2Good suffix rule finds the nearest substring matches the suffix before the mismatch
3S: - - - - - b b x
4 | | |
5P: (b b) - x - (b b) aWe can see that Boyer-Moore, while being more complicated than KMP, utilizes more information both from the target string and pattern. Given a long pattern, especially when there are repeated subpatterns (like a DNA sequence), Boyer-Moore should in theory out-perform KMP. Another question is whether KMP is indeed much inferior to Boyer-Moore in practice. I performed two tests for the three algorithms: 1) Boyer-Moore, 2) KMP Z-based, and 3) KMP vanilla.
To make a fair comparison of run time, I only calculated the run time for the actual matching step, but not the preprocessing step. I assume the preprocessing time is Boyer-Moore > KMP Z-based > KMP vanilla. However, in practice, preprocessing time should be considered.
Test
The first task is to search ~ 10000 most common English words (link) in the Shakespeare complete works (link), which contains around 5.5 million characters. All English words are lower-case. The character table used in Boyer-Moore contains only 26 lower-case letters. The second task is to locating ~ 5000 randomly generated sequences (from Bioinformatics.org) in human chromosome 20. The character table used in Boyer-Moore is just “acgt”.
- Task 1: Search ~ 10000 most common English words in Shakespeare complete works
- Task 2: Search ~ 5000 random DNA sequences of length varied from 4 to 100 basepair in human chromosome 20
Result
In task 1, I plot the run time for three methods against the word length. We noticed that Boyer-Moore is significantly slower than KMP for shorter words (< 5 chars). Boyer-Moore’s run time is reversely related to the word length and starts to catch up with KMP at word length of 10, and even out-performs KMP for very long words (> 16 chars). In practice, users may often want to search sentences or even paragraphs. In those cases, Boyer-Moore should be much faster than KMP. For shorter words, Boyer-Moore’s performance is not that bad. So it’s fair to say that KMP is slower than Boyer-Moore in practice.
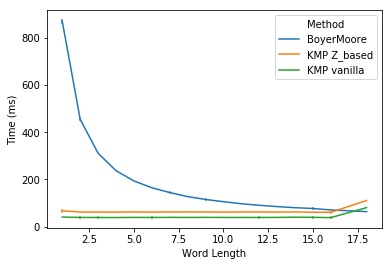
It should be unsurprising that Boyer-Moore is faster than KMP for task 2. Because for DNA sequences which are made up of only four letters, one would expect many repeated subpatterns, where the good suffix rule shines. However, it is a bit surprising that Boyer-Moore is slower than vanilla KMP for all DNA sequences except for sequences of 51-bp long (might be due to a big skip in those sequences).
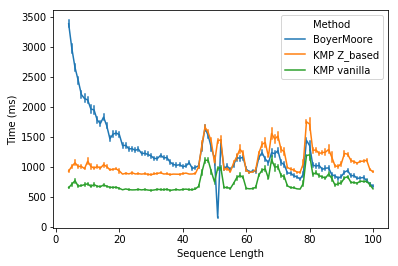
In conclusion, Boyer-Moore is slower than KMP for very short patterns, but shows increased performance as the pattern length increases. It’s surprising to find that the vanilla KMP is not only simple but also very fast in both tasks. I’m sure there is plenty of room for optimization of my C++ implementation of Boyer-Moore to further reduce the gap between Boyer-Moore and KMP at shorter patterns. I’m also curious about the algorithm being used in the search function of Microsoft WORD, or any other softwares.
Update (2019-4-7): It seems that there are simpler (maybe faster) ways to implement Boyer-Moore.
- [1]. A great resource for all kinds of string matching algorithms.
- [2]. A C implementation of Boyer-Moore in HTSlib based on notes in [1].